How daily compounding works in case of inverse and leveraged ETFs?

Daily compounding

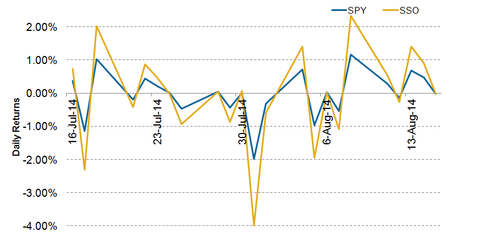
As we explained earlier in this series, leveraged ETFs seek to deliver daily returns in multiples (typically 2x or 3x) of the returns on an underlying index. For example, the ProShares Ultra S&P 500 (SSO) seeks to generate twice the daily returns of the S&P 500 (VOO), before fees and expenses. The fund has invested in Apple (AAPL) and Microsoft (MSFT). However, a large chunk of its holdings are in the form of swap agreements with financial institutions. For example, the fund entered into a swap agreement on the SPDR S&P 500 ETF (SPY) with Deutsche Bank under which the fund received twice the return on SPY on a given day. As you can see in the chart below, the ProShares Ultra S&P 500 (SSO) has given almost twice the daily returns on SPY every day.

So, if SPY rises 10% on a given day, the fund seeks to provide 20% returns to investors before fees and expenses. If that’s the case, shouldn’t SSO generate twice the returns generated by SPY over a longer term?

The reality seems to be different due to the phenomenon of compounding at play. Let’s look at the following three cases to understand how compounding works in leveraged ETFs.

Case 1: (1+10%)(1+10%)=(1+21%)—A continuous uptrend

If SPY rises 5% each on two consecutive days, SSO will rise 10% each day due to the 2x leverage achieved using derivative products and external borrowings. While the compounding works even for SPY, it’s magnified in SSO due to the 2x multiplier effect. Assuming the initial price of both SPY and SSO is $100, SPY will be worth $110.25 (10.25% returns) while SSO will be $121 (21% returns) at the end of Day 2. So, the average returns on leveraged funds during a continuous uptrend tend to outperform their multiplier. In this case, the fund has generated more than 2x returns (21.00/10.25) over two days.

Case 2: (1-10%)(1-10%)=(1-19%)—A continuous downtrend

Now consider a situation where SPY drops by 5% each on two consecutive days. Due to the 2x leverage, SSO will drop 10% on each of those days. Assuming an initial price of both SPY and SSO of $100, SPY will be worth $90.25 (-9.75% returns), while SSO will be $81 (-19% returns) at the end of Day 2. So, the average losses on leveraged funds during a continuous downtrend are typically lower than the multiplier. In this case, the fund has generated less than 2x losses (19/9.75) over two days.

Case 3: (1+10%)(1-10%)=(1-1%)—A volatile market

If SPY rises 5% on Day 1 and falls 5% on Day 2, SSO will go up 10% on Day 1 and fall 10% on Day 2 due to the 2x leverage. Assuming an initial price of both SPY and SSO of $100, SPY will be worth $99.75 (-0.25% returns) while SSO will be $99 (-1% returns) at the end of Day 2. So, the average returns on leveraged funds during volatility tend to underperform the multiplier. In this case, the fund has generated 4x losses (1.00/0.25) over two days.

From the third case, we can see that in a non-trending volatile market, the fund can lose money even if the index stays at the original level.

To find out how leveraged ETFs rebalance their portfolios daily, read on to the next part of this series.